記事一覧

AVL木の性質

2025-04-20

はじめに

平衡二分探索木の実装と使い分けを整理したくなったので、簡潔にまとめる。
数あるバリエーションのうち、本記事では

に絞って解説する。 赤黒木や Treap などの他の平衡二分探索木については後日記事を追加する予定。

参考文献は主に『アルゴリズムイントロダクション』（第3版和訳）と Sedgewick & Wayne『Algorithms, 4th Edition』を参照。誤りがあれば指摘求む。

基本概念

ノードの構造とバランス係数

高さの上界

頂点数 n の AVL 木の高さは 1.44log⁡2(n+1)1.44\log_2(n+1) 未満になる

ラフな証明

m(h)m(h) を高さ h の AVL 木の最小の接点数とする このとき m(1) = 1, m(2) = 2, 任意の h > 2 に対して m(h) = m(h - 1) + m(h - 2) + 1 (高さ h の AVL 木は左右の部分木が h-1 と h-2 の AVL 木になるため) これはフィボナッチ数列の定義と非常に似ている (F0=0,F1=1,Fh+2=Fh+1+FhF_0 = 0, F_1 = 1, F_{h+2} = F_{h+1} + F_h) FhF_h を h 番目のフィボナッチ数とすると,

m(1)=1=F3−1,m(2)=2=F4−1.m(1) = 1 = F_3 - 1, m(2) = 2 = F_4 - 1.

任意の h > 2 について

m(h)=m(h−1)+m(h−2)+1=(Fh+1−1)+(Fh−1)+1=Fh+2−1\begin{align} m(h) = m(h-1) + m(h-2) + 1 = (F_{h+1} - 1) + (F_h - 1) + 1 = F_{h+2} - 1 \end{align}

Fh=(1+52)h−(1−52)h5F_h = \frac{(\frac{1+\sqrt{5}}{2})^h - (\frac{1-\sqrt{5}}{2})^h}{\sqrt{5}}より, 頂点 n 高さ h の AVL 木について

n≥m(h)=Fh+2−1=(1+52)h+2−(1−52)h+25n \ge m(h) = F_{h+2} - 1 = \frac{(\frac{1+\sqrt{5}}{2})^{h+2} - (\frac{1-\sqrt{5}}{2})^{h+2}}{\sqrt{5}}

計算すると h>1.44log⁡2(n+1)h > 1.44 \log_2(n+1)

BST との違い・メリット
視点 二分探索木(未平衡) AVL 木 備考
高さ n 1.44l\og2(n)1.44l\og_2(n)
探索速度 最悪n 常に O(log⁡2(n))O(\log_2(n))
更新コスト ほぼ0 高さ計算+回転

回転パターンの図解

次は回転について説明する。 平衡二分探索木では、木の順序(左ノード < 親ノード < 右ノード) を 壊さずに高さを整えるために回転という操作を行う。 AVL 木で実際に必要な回転は次の 4 パターンだけ。

LL（右回転）

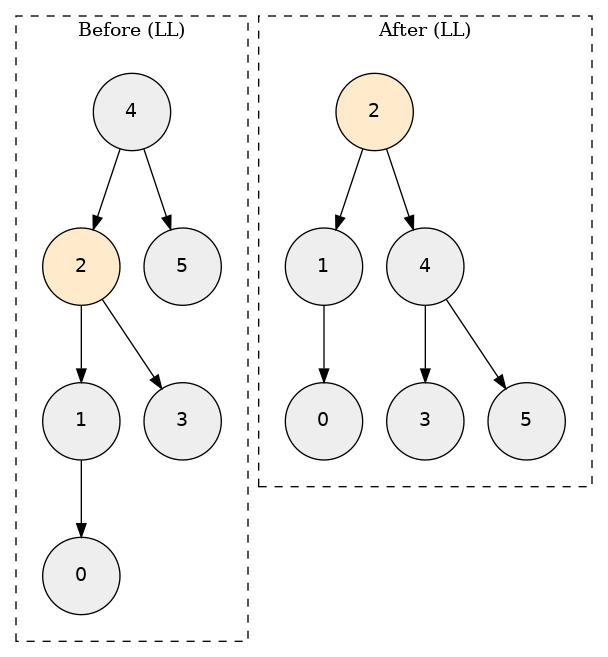
LL.png

色付きのノードを右に回転する

  1. 4 の左の子を 2 の右の部分木(3)につけ直す
  2. 2 をルートにして、4 を 2 の右の子として接続する
  3. 4 -> 2 の順に高さ/バランス係数を再計算する

RR（左回転）

LL(右回転)を逆にしただけ。 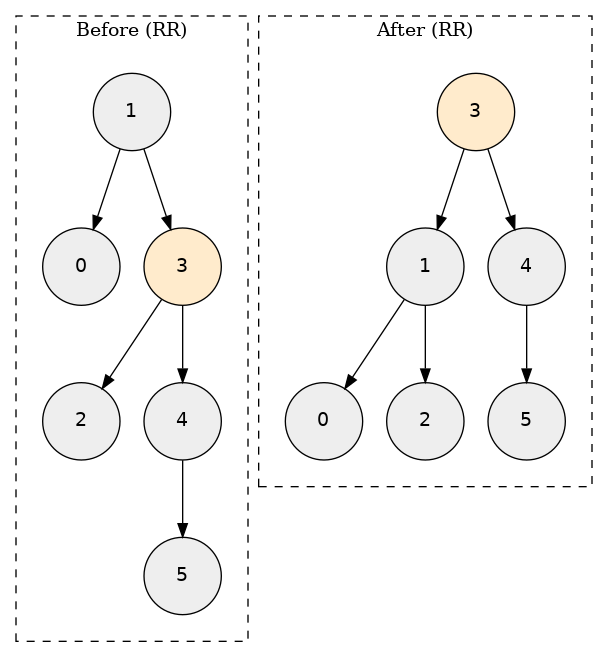RR.png 手順は

  1. 1 の右の子を 3 の左の部分木(2)につけ直す
  2. 3 をルートにして、1 を 3 の左の子として接続する
  3. 1 -> 3 の順に高さ/バランス係数を再計算する

LR（左‑右回転）

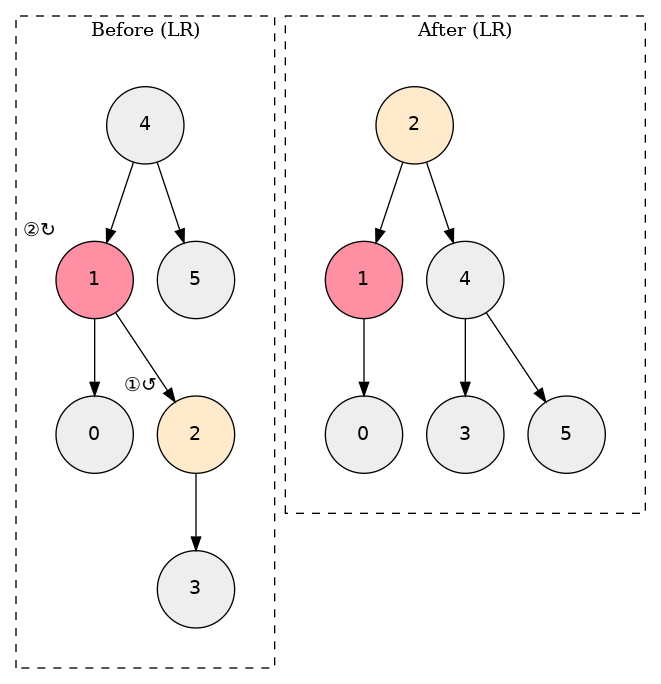
左のノードの右部分木が伸びているパターン。 １回右回転してLLのパターンにしてから左に回転してバランスを取る。 LR.png

RL（右‑左回転）

実装(C++)

ノードと木の定義

template <typename T>
struct AVLNode {
    T data;
    AVLNode* left  = nullptr;
    AVLNode* right = nullptr;
    int8_t balance = 0;   // -1 <= balance <= 1
};

template <typename T>
class AVLTree {
    public:
        void insert(const T& key);
        void erase(const T& key);
        bool search(const T& key) const;
        void clear();
    private:
        AVLNode<T> *root = nullptr;
        int height(AVLNode<T>* n) const;
        void update(AVLNode<T>* n);
        AVLNode<T> *rotateLeft(AVLNode<T> *x);
        AVLNode<T> *rotateRight(AVLNode<T> *y);
        AVLNode<T> *rebalance(AVLNode<T> *n);
        AVLNode<T> *insertImpl(AVLNode<T> *n, const T& key);
        AVLNode<T> *eraseImpl(AVLNode<T> *n, const T& key);
    
};

挿入

template<typename T> 
  void AVLTree<T>::insert(const T& key) {
  root = insertImpl(root, key);
}

template<typename T>
  AVLNode<T>* AVLTree<T>::insertImpl(AVLNode<T> *n, const T& key) {
  if (n == nullptr) {
    return new AVLNode<T>(key, nullptr, nullptr, 0);
  }
  if (n->data > key) {
    n->left = insertImpl(n->left, key);
  } else if (n->data < key) {
    n->right = insertImpl(n->right, key);
  } else {
    return n;
  }  
  n->bal = height(n->left) - height(n->right);

  return rebalance(n);
}

削除

探索

テスト用 main と assert

ユースケースと実務採用例

8. 参考文献・リンク集